题解 P2911 【[USACO08OCT]牛骨头Bovine Bones】

写在最前：本人是刚入门的菜鸡，所掌握的概率知识也仅限于初中水平（不会期望），还请各位大佬多多喷我的垃圾题解 XD ## 题意简述 现有三个不同的骰子，面数分别为 $s_1,s_2,s_3$。对于一个有 $S$ 个面的骰子每个面上的数字是 $1,2,3,…,S$，每个面（上的数字）出现的概率均等。我们需要求出哪个所有“三个面上的数字的和”出现得最频繁。如果有很多个和出现的概率相同，那么只需要输出最小的那个。 数据范围：$2\le s_1\le20,2\le s_2\le20,2\le s_3\le40$ ## 思路讲解 看到这么小的数据范围，那当然是暴力枚举啦！况且这还是入门题，怎么可能如此难为我这种萌新呢。但是我的神仙同学说：  于是我~~把自己的头发都抓光了，~~ 终于用 $O(1)$ 过了这道题。 由于接下来的讲解可能略显冗长，这里先放一张我写的简化版的题解的图片（原是写给我的神仙同学看的），如果你看懂了那就可以不用看下面的讲解了。  好了，不管你是因为我写得过于晦涩、简略而没看懂，还是因为我的字写得太丑而不屑一看，抑或是好奇我的详细讲解有多啰嗦，你一定是准备开始看下文了。那么接下来正文就要开始了！ 事实上第一眼看到这个题目，我立刻想到了自己小学时在某本数学趣味书上看到的一个喜欢赌博的数学家，他玩过这样一个游戏：掷两个骰子（正方体的那种），两个人分别对两个骰子的点数之和进行猜测，谁猜对了谁赢。而他发现：在这样的规则下，猜7胜率最高。于是他凭着这个发现赢了好多钱。~~但现在我觉得这个故事很可能是假的（）~~ 根据这个发现，很自然地，我们先研究两个骰子的情况。对于上述问题，我们可以列个表来解决： | | 1 | 2 | 3 | 4 | 5 | 6 | | - | - | - | - | - | - | - | | **1** | 2 | 3 | 4 | 5 | 6 | 7 | | **2** | 3 | 4 | 5 | 6 | 7 | 8 | | **3** | 4 | 5 | 6 | 7 | 8 | 9 | | **4** | 5 | 6 | 7 | 8 | 9 | 10 | | **5** | 6 | 7 | 8 | 9 | 10 | 11 | | **6** | 7 | 8 | 9 | 10 | 11 | 12 | 可以观察到，7出现的次数最多。再想一想，就可以知道：当掷出两个相同的骰子时，若骰子有 $n$ 个面，则概率最大的和为 $1+n$。 接下来看一看当两个骰子面数不一样时会怎样（事实上大部分人应该已经能够得出亿些结论了，但我太菜了，只好继续研究）。仍然采用列表法，我们用面数分别为5和8的骰子试试看： | | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | | - | - | - | - | - | - | - | - | - | | **1** | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | | **2** | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | | **3** | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | | **4** | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | | **5** | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 根据这个表格，我们可以得出较为一般的结论了 ~~（明明根据上个表格就行了）~~ 。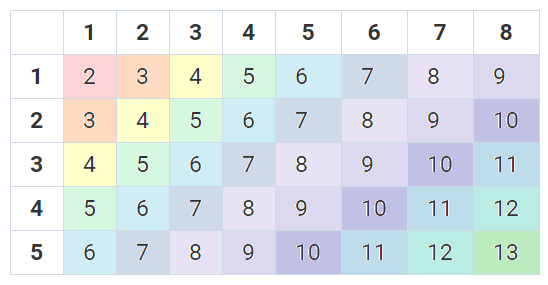为了更清楚地说明，我给这张表格上了色：  好了！现在任何人都能毫无障碍地看出其中的规律，不用说大家应该也知道，但我还是啰嗦一下~~免得过不了审核~~： 若有两个骰子，它们的面数分别为 $a,b$（ $a\le b$），则可以得出以下结论： - 不同的点数之和的情况总数为 $a+b-1$，从小到大具体是 $2,3,4,...,a+b$； - 点数之和出现次数最多的是 $1+a,1+a+1,1+a+2,...,1+b$，且总共有 $b-a+1$个出现次数最多的和； - 当和为 $m$ 的出现次数不是最多时，设 $m$ 的出现次数为 $f(m)$，则 $f(m+1)=\begin{cases}f(m)+1&m<1+a\\f(m)-1&m>1+b\end{cases}$ $f(m-1)=\begin{cases}f(m)-1&m<1+a\\f(m)+1&m>1+b\end{cases}$ 进行到这里，我们已经把两个骰子的问题研究得较为清楚了。事实上，最重要的结论是第二条，因为题目只要求我们求出和，而并不要求知道这个和出现的次数（或概率）。 接下来，我们加入第三个骰子。 --- 如果现在在原来的表格的基础上直接加入一个骰子，那我们将会得到一个长方体，那样不太利于我们的思考（事实上这个长方体中数字的分布也有着和上文表格类似的规律，具体是怎样的请读者自行想象）。因此我们对这个表格再简化一下。由于我们只关心骰子的点数之和，并不关心这个和是如何得出的，**我们可以将两个骰子构成的表格压缩成一条线段**。根据上面的第一条结论，这条线段的长度应为 $a+b-1$（仍然设两个骰子的面数分别为 $a,b$）。我们在这条线段上从左往右把 $2,3,4,...,a+b$ 都标上，这样我们的压缩就完成了！为了便于说明，我们把这条线段叫做 $AB$。~~这个图大家应该想象得出来，我就不画了（）~~ 但这样的表示还是有很明显的缺陷，大家也一定能看出来，那就是这条线段上没有各个和出现次数的信息。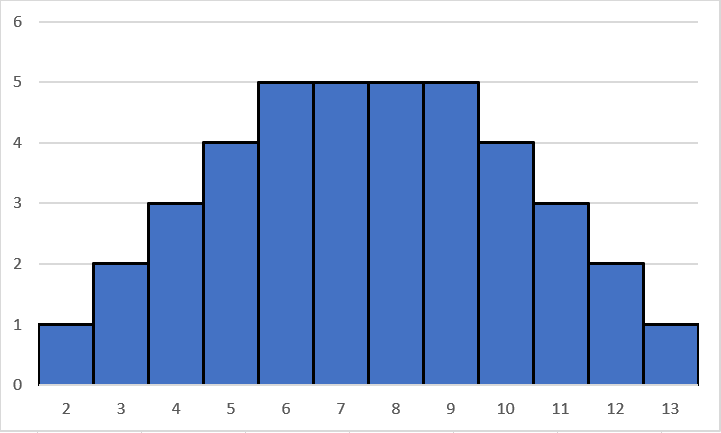没关系，我们可以把它变成一个柱状图：  这其实类似于频数分布直方图，但并不真的是。当我们做完这一步工作以后，再加入第三个骰子，事情将会变得容易许多。我们设这个骰子有 $c$ 个面，那么利用刚才的线段 $AB$，我们又可以画出一个表格，但这个表格上关于和的出现次数的信息是不准确的，因此它其实不太重要。最重要的是接下来的这一步，请让你的脑子转起来！ 仍然要使用刚才的线段 $AB$，或者使用上述柱状图的横轴，对于上面的每个数字，我们可以给它加上 $1$ 或 $2 $ 或 $...$或 $c$，这样就得到三个骰子的点数之和。若是要得到相同的和，我们随意选取线段上的一个点，给这个点所对应的数加 $1$，给它左边相邻的数加 $2$，再左边的数加 $3$……，以此类推。通过这样的方法，我们得到的和都是相等的。事实上我们可以把这样的过程想象成**一条长度为 $\mathbf{c}$ 的线段 $\mathbf{s}$ 在线段 $\mathbf{AB}$ 上滑动，线段 $\mathbf{s}$ 上的数从右到左是 $\mathbf{1,2,...,c}$**，不过线段 $s$ 不一定完全被包含在 $AB$ 内，它也可以部分滑到外面。如果理解了这一步，我们就非常接近最终答案了！由于线段 $AB$ 上每一个数的出现次数并不相同，那么很容易想到，当线段 $s$ 在比较靠中间的位置上时，所得出的相同的和的个数会比较多。更进一步地，要使相同的和的个数最多（这正是题目所求的！），我们应使线段 $s$ 最多地落在 $\left[1+a,1+b\right]$ 这个范围内。由此，我们已经可以得出最终答案了！ 当线段 $s$ 的长度不足以完全覆盖 $\left[1+a,1+b\right]$ 或恰好完全覆盖（即 $c\le b-a+1$）时，为了使和最小（题目要求），我们要尽量使它靠左。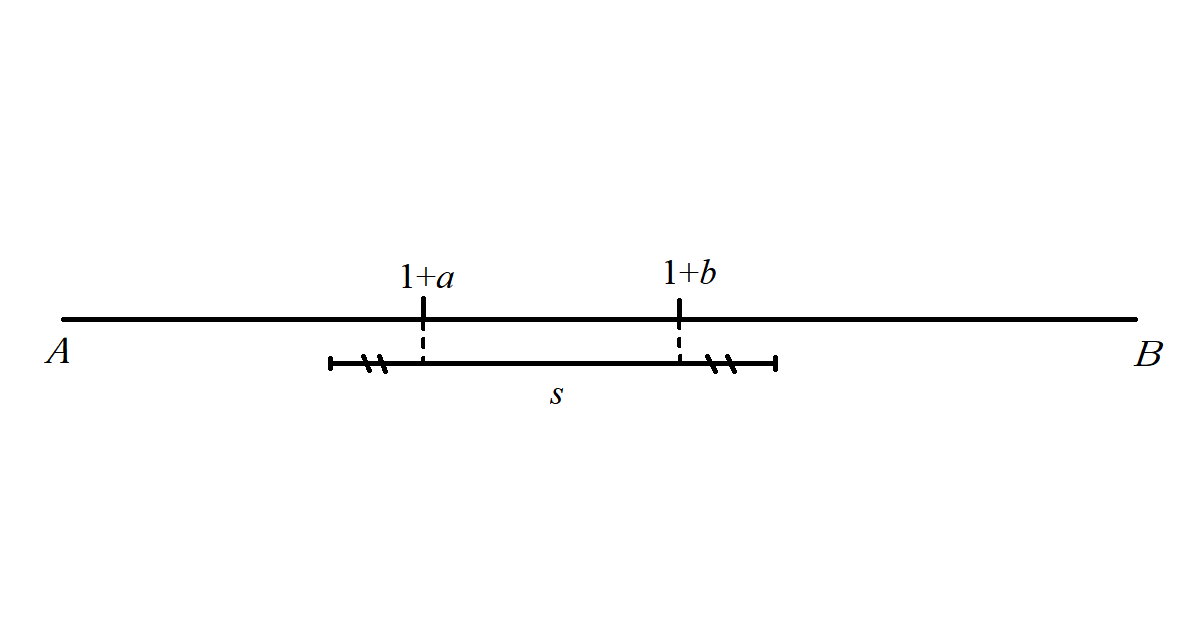具体来讲，我们要使它的左端点与 $1+a$ 重合，那么答案就是 $1+a+c$； 当线段 $s$ 的长度比 $\left[1+a,1+b\right]$ 更大（即 $c>b-a+1$）时，同理仍应使它尽量靠左，但也要保证尽量靠中间，那么此时线段 $s$ 在线段 $AB$ 上应该是这样一种状态：  当然这里 $c-\left(b-a+1\right)$ 除以2不一定是整数，那么根据尽量靠左的原则，可以给左边多分配一点，答案应为 $1+b+\left\lfloor\dfrac{c-(b-a+1)}{2}\right\rfloor+1$。（这里的 $\left\lfloor\right\rfloor$ 是下取整符号，即 $\left\lfloor{x}\right\rfloor$ 表示小于等于 $x$ 的最大整数） 好啦，我们几乎大功告成啦！为什么是几乎呢，因为这里 $a,b,c$ 的大小关系还不明确（当然你也可以求三次后取最小值），我们回头看看只有两个骰子时的情况： >点数之和出现次数最多的是 $1+a,1+a+1,1+a+2,...,1+b$，且总共有 $b-a+1$个出现次数最多的和； 要使出现次数最多，那么 $b-a$ 应最大，对于三个骰子的情况同样如此（这里还是需要稍微思考一下的），这样我们很容易得出 $b$ 应取为三个数中最大的数，$a$ 应取为三个数中最小的数，$c$自然就是中间的那个数。至此，我们已经完全解决了这个问题！ ## 最后附上代码 ```cpp #include<iostream> #include<math.h> using namespace std; void swap(int &x,int &y) //swap必须加上&取地址才能真正交换，类型必须写void { int t=x; x=y; y=t; } int main() { int a,b,c; cin>>a>>b>>c; if(a<b) swap(a,b); if(b<c) swap(b,c); if(a<b) swap(a,b); //冒泡排序 if(b<=a-c+1) cout<<1+b+c; else cout<<2+a+(b-a+c-1)/2;//int除法自动下取整 return 0; } ``` 需要说明的是，这种方法也可以求出和的出现次数（概率），当然式子长得不太好看就是了，大家可以自己想一想哦！（明明想都不用想） Update: 2020/8/6 修改了巨丑无比的代码 Update: 2020/11/29 代码和LaTeX有点小锅，修一修